双曲线准线公式
双曲线准线公式：x^2/a^2-y^2/b^2=1
在圆锥曲线的统一定义中：平面内一点到定点与定直线的距离的比为常数e（e>0）的点的轨迹，叫圆锥曲线。而这条定直线就叫做准线（Directrix）。
一般的，双曲线（希腊语“ὑπερβολή”，字面意思是“超过”或“超出”）是定义为平面交截直角圆锥面的两半的一类圆锥曲线。它还可以定义为与两个固定的点（叫做焦点）的距离差是常数的点的轨迹。
双曲线的准线是什么？
双曲线的准线的方程就是：y=±a²/c。
其中a是实半轴长，b是虚半轴长，c是半焦距。
双曲线的准线的方程：
1、双曲线。
双曲线：（x^2/a^2)-(y^2/b^2)=1。
准线方程为：x=±a^2/c。
2、椭圆。
(x^2/a^2)+(y^2/b^2)=1（a>b>0）。
准线方程为：x=±a^2/c。
圆锥曲线上任意一点到一焦点的距离与其对应的准线（同在Y轴一侧的焦点与准线）对应的距离比为离心率。椭圆上任意一点到焦点距离与该点到相应准线距离的比等于离心率e。
双曲线的准线是什么？怎么得来的？谢谢！
平面内到一个定点与一条定直线的距离之比是一个大于1的常数的动点的轨迹是双曲线，这个常数即该双曲线的离心率，定点是双曲线的焦点，定直线是双曲线的准线。
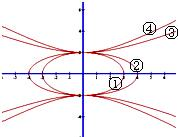
双曲线有两条准线L1（左准线），L2（右准线），准线与双曲线的位置关系如图所示。
以原点为中心的双曲线
的准线的方程就是：x=±a²/c。
扩展资料
几何性质：
准线到顶点的距离为Rn/e，准线到焦点的距离为P = Rn(1+e)/e = L0/e 。
当离心率e大于零时，则P为有限量，准线到焦点的距离为P = Rn(1+e)/e = L0/e 。
当离心率e等于零时，则P为无限大，P是非普适量。用无限远来定义圆锥曲线是不符合常理的。
教科书中定义局限性的原因是不了解准线的几何性质，当e等于零时则准线为无限远，准线是非普适量，是局限性的量。
参考资料来源：百度百科-双曲线准线
双曲线准线的方程
双曲线有两条准线L1（左准线），L2（右准线），准线与双曲线的位置关系如右图所示。
以原点为中心的双曲线 的准线的方程就是：x=±a²/c；
以原点为中心的双曲线 的准线的方程就是：y=±a²/c；
其中a是实半轴长，b是虚半轴长，c是半焦距。（ ）
例如，存在以原点为中心的双曲线 按照以上计算公式，则其准线方程为：
L1的方程： ；L2的方程： 。
