一、布拉格公式
布拉格公式是2dsinθ=nλ,d为晶面间距,θ为衍射半角,对于X射线衍射,当光程差等于波长的整数倍时,晶面的散射线将加强,布拉格方程是X射线在晶体产生衍射时的必要条件而非充分条件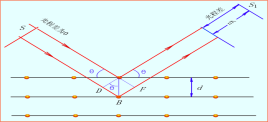
有些情况下晶体虽然满足布拉格方程,但不一定出现衍射,即所谓系统消光。当晶面与X射线之间满足上述几何关系时,X射线的衍射强度将相互加强。它简单明确地阐明衍射的基本关系,应用非常广泛。用已知波长的X射线去照射未知结构的晶体,通过衍射角的测量求得晶体中各晶面的间距d,从而揭示晶体的结构,这就是结构分析。
二、布拉格衍射的条件
晶格对电磁波的衍射和布拉格条件
晶格对电磁波的衍射,可以看作多个晶面对电磁波的反射的相干叠加。通常有两种不同方式考虑这种相干叠加,一种方式是固定晶面(例如只考虑简单晶面),考虑反射时可以以不同角度入射,而不同晶面间的反射如果正好相差波长整倍数时相干加强;另一种方式是只考虑与入射方向垂直的晶面,如果这样的晶面间距为半波长的整数倍则相干加强。两种方式得到的相干加强条件等价,称为布拉格条件。
三、布拉格衍射有哪些条件,布拉格衍射条件对声光调制实验有何知道意义
布拉格方程:对于X射线衍射,当光程差等于波长的整数倍时,晶面的散射线将加强,此时满足的条件为2dsinθ=nλ---布拉格方程,其中,d为晶面间距,θ为入射线,反射线与反射晶面之间的夹角,λ为波长,n为反射级数,布拉格方程是X射线在晶体产生衍射时。
四、布拉格反射原理
假设入射波从晶体中的平行原子平面作镜面反射,每个平面反射很少一部分辐射,就想一个轻微镀银的镜子一样。再这种类似镜子的镜面反射中,其反射角等于入射角。当来自平行原子平面的反射发生相长干涉时,就得出衍射束。考虑间距为d的平行晶面,入射辐射线位于纸面平面内。相邻平行晶面反射的射线行程差是2dsinx,式中从经面开始量度。当行程差是波长的整数倍时,来自相继平面的辐射就发生了相长干涉。 这就是布拉格定律。布拉格定律用公式表达为:2dsinx=n/f (d为平行原子平面的间距,f为入射波频率,x为入射光与晶面之夹角)布拉格定律的成立条件是波长小于2d来自






