一、加权算术平均数和加权调和平均数的区别和联系
加权算术平均数和加权调和平均数的区别和联系
加权算术平均数一般用在未知分子的情况下,即总体标志总量未知.
调和算术平均数一般用在未知分母的情况下,即总体单位数未知
二、加权算术平均数与加权调和平均数有何区别和联系
加权平均值即将各数值乘以相应的权数,然后加总求和得到总体值,再除以总的单位数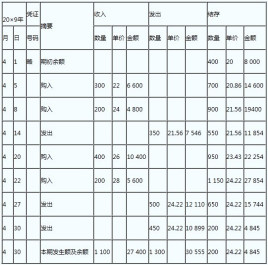 举例:
举例:
下面是一个同学的某一科的考试成绩:
平时测验 80, 期中 90, 期末 95
学校规定的科目成绩的计算方式是:
平时测验占 20%
期中成绩占 30%
期末成绩占 50%
这里,每个成绩所占的比重叫做权重。那么,
加权平均值 =( 80*20% + 90*30% + 95*50% )/(20%+30%+50%)=90.5
权调和平均数
适用于分组资料的计算,其计算公式为:
平均数=(M1+M2+…+Mn)/(M1/X1+M2/X2+…+Mn/Xn)=∑Mi/∑(Mi/Xi)
具体计算方法如下:
(1)先计算出各个变量值的倒数,即1/X;
(2)计算上述各个变量值倒数的算术平均数,即[∑(1/X)]/n;
(3)再计算这种算术平均数的倒数,即n/[∑(1/X)],就是调和平均数。
三、加权算术平均数和调和平均数有什么不同
调和平均数
harmonic
mean
调和平均数是平均数的一种。但统计调和平均数,与数学调和平均数不同。
在数学中调和平均数与算术平均数都是独立的自成体系的。计算结果两者不相同且前者恒小于后者。
因而数学调和平均数定义为:数值倒数的平均数的倒数。但统计加权调和平均数则与之不同,它是加权算术平均数的变形,附属于算术平均数,不能单独成立体系。且计算结果与加权算术平均数完全相等。
主要是用来解决在无法掌握总体单位数(频数)的情况下,只有每组的变量值和相应的标志总量,而需要求得平均数的情况下使用的一种数据方法。
公式:n/(1/A1+1/A2+...+1/An)
加权平均数
Weighted
average
加权平均数是不同比重数据的平均数,加权平均数就是把原始数据按照合理的比例来计算,若
n个数中,x1出现f1次,x2出现f2次,…,xk出现fk次,那么(x1f1
+
x2f2+
...
xkfk)÷
(f1
+
f2
+
...
+
fk)
叫做x1,x2,…,xk的加权平均数。f1,f2,…,fk是x1,x2,…,xk的权。
公式:(x1f1
+
x2f2+
...
xkfk)/n,其中f1
+
f2
+
...
+
fk=n,f1,f2,…,fk叫做权。
说明:1)“权”的英文是weight,表示数据的重要程度。即数据的权能反映数据的相对“重要程度”。
2)
平均数是加权平均数的一种特殊情况,即各项的权相等时,加权平均数就是算术平均数。
四、什么时候用加权算术平均数,什么时候用加权调和平均数?
加权平均值即将各数值乘以相应的权数,然后加总求和得到总体值,再除以总的单位数。加权平均值的大小不仅取决于总体中各单位的数值(变量值)的大小,而且取决于各数值出现的次数(频数),由于各数值出现的次数对其在平均数中的影响起着权衡轻重的作用,因此叫做权数。
加权调和平均数是加权算术平均数的变形。它与加权算术平均数在实质上是相同的,而仅有形式上的区别,即表现为变量对称的区别、权数对称的区别和计算位置对称的区别。因而其计算公式为:
算术平均数和调和平均数是平均指标的两种表现形式。算术平均数和调和平均数并非两类独立的平均数;算术平均数和调和平均数的数值之间并无直接关系,也不存在谁大谁小的问题;不能根据同一资料既计算算术平均数,又计算调和平均数,否则就是纯数字游戏,而非统计研究。
加权调和平均数的应用: 在很多情况下,由于只掌握每组某个标志的数值总和(M)而缺少总体单位数(f)的资料,不能直接采用加权算术平均数法计算平均数,则应采用加权调和平均数。
五、加权调和平均数是什么?
加权调和平均数如下:
这里所谓的“加权调和平均数”是按照调和平均数的定义,各变量值倒数的加权算术平均数的倒数。也是调和平均数的一种。一般而言,统计加权调和平均数有不同,它是加权算术平均数的变形,附属于算术平均数,不能单独成立体系。
加权调和平均数的额计算:
根据资料的不同,调和平均数可分为简单调和平均数和加权调和平均数两种。其中加权调和平均计算如下:
先计算出各个变量值的倒数,即1/X。
计算上述各个变量值倒数的算术平均数,即[∑(1/X)]/n。
再计算这种算术平均数的倒数,即n/[∑(1/X)],就是调和平均数。